【Alg】 最大子矩形 & 【Sol】 P1578 奶牛浴场

前言

自创的一种题解区最简洁的做法，运用了奇妙的加点操作。

这题是最大子矩形模板题，我用的是障碍点找子矩形。

我在做这题的时候参考了题解区的 这篇题解 ，然后我自己写的时候发现后两种情况可以直接优化掉，于是我的做法就只有一遍排序和遍历。

题解

基本思路

最大子矩形四条边都不能向外拓展，所以说四条边上一定都有至少一个障碍点。

考虑枚举左边界上的障碍点和右边界上的障碍点，然后在枚举过程中维护上下边界。

具体来说：

先对所有按横坐标排序，点固定点为左边点，向右枚举点为右边点。

假设我们已经知道了上边界为，下边界为，则此时这个矩形的面积就是，更新答案。

维护上下边界也很简单，因为我们是从左往右枚举的，所以可以在枚举的时候来更新上下边界：若当前枚举完的在上面，则更新上边界，反之更新下边界。

形式化的说：若，则，否则。

特殊情况

(1) 上下边界为整个农场的上下边界

每枚举一个时上边界设为，下边界设为。

(2) 覆盖农场角落

四个角落各方一个点。

(3) 左右边界为整个农场的左右边界

这里我使用了一种创新性的方法，减少了一次排序和循环遍历。

这样的矩形左右边界上没有点，那我们就考虑在这些矩形的左右边界上放点。

直接把边界上放满点就会爆炸，考虑怎么放点才能覆盖这样的所有矩形。

这些矩形虽然没有左右边界，那就意味着它一定有上下边界，那我们直接把上下边界上的点往左右边界上放就行了。

具体方法是：在输入一个点时把和也加进去。

复杂度 & 注意事项

时间复杂度。

注意空间开三倍以上，因为我们多加了一些点进去。

代码

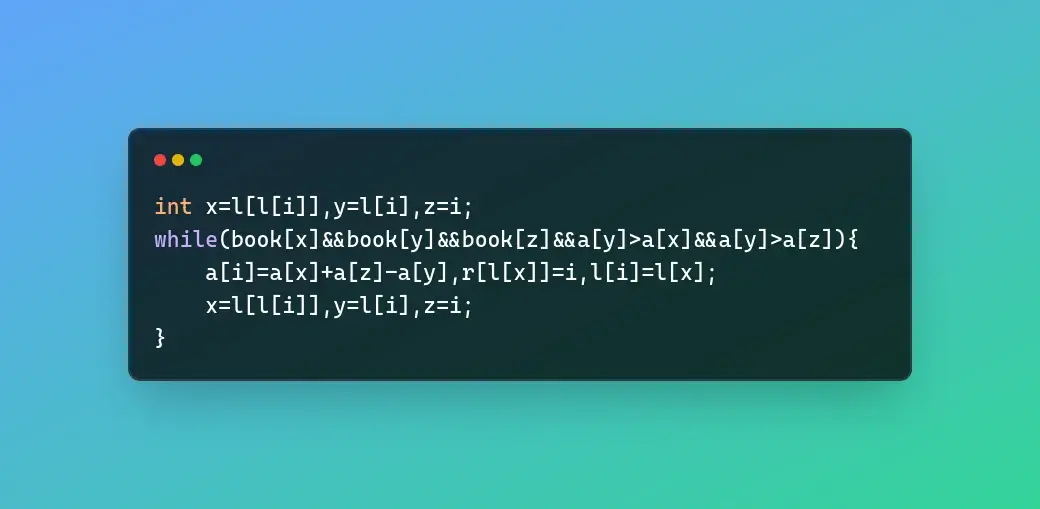
丑就丑吧，我也懒得改码风了。

#include <bits/stdc++.h>
using namespace std;
const int N=2e4+10;
int l,w,n,cnt,ans,_up,_down;
struct point{int x,y;}a[N];
inline bool cmp(point a,point b){
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>l>>w>>n,cnt=n;
    for(int i=1;i<=n;i++){
        int x,y;cin>>x>>y;
        a[i]={x,y},a[++cnt]={0,y},a[++cnt]={l,y};
    }
    n=cnt,a[++n]={0,0},a[++n]={0,w},a[++n]={l,0},a[++n]={l,w};
    sort(a+1,a+n+1,cmp);
    for(int i=1;i<n;i++){
        _up=w,_down=0;
        for(int j=i+1;j<=n;j++){
            ans=max(ans,(a[j].x-a[i].x)*(_up-_down));
            if(a[j].y>a[i].y)_up=min(_up,a[j].y);
            else _down=max(_down,a[j].y);
        }
    }
    cout<<ans;
    return 0;
}